Data di Pubblicazione 13/06/23 3.55
Trong bài viết này Hocvn sẽ hướng dẫn bạn Viết Phương Trình Đi Qua 2 Điểm Cực Trị Của Đồ Thị Hàm Số Bậc 3. Mời bạn đọc cùng theo dõi!
 Phương Trình Đi Qua 2 Điểm Cực Trị
Phương Trình Đi Qua 2 Điểm Cực Trị Cách Viết Phương Trình Đường Thẳng Đi Qua Hai Điểm Cực Trị Của Đồ Thị Hàm Số Bậc Ba
Cho hàm số bậc ba y=f(x)=ax3+bx2+cx+d với a≠0 có đồ thị gọi là đường cong (C) và
y′=f′(x)=3ax2+2bx+c
Nhận thấy y′ là một tam thức bậc hai có
Δ′y′=b2−3ac.
Do đó. có hai khả năng sau:
- Nếu Δ′≤0 thì hàm số không có cực trị.
- Nếu Δ′>0 thì hàm số có hai điểm cực trị. Khi đó, đồ thị hàm số cũng có hai điểm cực trị và phương trình đường thẳng đi qua 2 điểm này là
y=kx+m,
trong đó kx+m là phần dư khi chia đa thức ax3+bx2+cx+d cho 3ax2+2bx+c (tức là phần dư khi chia y cho y′).
Thật vậy, giả sử phương trình f′(x)=0 có hai nghiệm phân biệt x1,x2 thì ta có f′(x1)=f′(x2)=0 và toạ độ hai điểm cực trị của đồ thị hàm số có dạng A(x1;f(x1)), B(x2;f(x2)).
Thực hiện phép chia f(x) cho f′(x) và giả sử ta được thương q(x) và dư là r(x) (r(x) có dạng kx+m) tức là
f(x)=q(x)⋅f′(x)+r(x).
Suy ra,
f(x1)=q(x1)⋅f′(x1)+r(x1)=r(x1),
vì f′(x1)=0. Hay toạ điểm A là (x1,r(x1)). Tương tự tính được toạ độ điểm B là (x2,r(x2)).
Như vậy toạ độ hai điểm A,B đều thỏa mãn phương trình y=r(x)=kx+m hay đường thẳng y=kx+m chính là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số bậc ba đã cho.
 Phương Trình Đi Qua 2 Điểm Cực Trị
Phương Trình Đi Qua 2 Điểm Cực Trị Ví Dụ Minh Họa Phương Trình Đi Qua 2 Điểm Cực Trị Của Đồ Thị Hàm Số Bậc 3
Tìm m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2x3 + 3(m – 1)x2 + 6(m – 2)x – 1 song song với đường thẳng y = -4x + 1.
Lời giải
Ta có y’ = 6x2 + 6(m – 1)x + 6(m – 2)
Hàm số có cực trị ⇔ y’ = 0 có 2 nghiệm phân biệt
⇔ Δ’ > 0 ⇔ 9(m – 1)2 – 36(m – 2) > 0 ⇔ 9(m – 3)2 > 0 ⇔ m ≠ 3
Thực hiện phép chia y cho y’ ta có phương trình đường thẳng đi qua 2 điểm cực trị là:
d: y = (-m2 + 6m – 9)x – m2 + 3m – 3
Khi đó d song song với đường thẳng y = -4x + 1
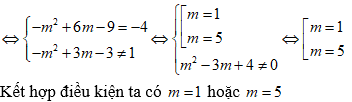
 Phương Trình Đi Qua 2 Điểm Cực Trị
Phương Trình Đi Qua 2 Điểm Cực Trị Cho hàm số y=−x3+3mx2+3(1−m2)x+m3−m2. Viết phương trình đi qua hai điểm cực trị của hàm số đã cho.
Bài giải:
Ta có: y′=−3×2+6mx+3(1−m2).
Phương trình y′=0 có Δ′=9>0, với mọi m ⇒ đồ thị hàm số đã cho luôn có hai điểm cực trị (x1;y1),(x2;y2).
Chia y cho y′ ta được: y=(13x−m3)y′+2x−m2+m.
Khi đó: y1=2×1−m2+m; y2=2×2−m2+m.
Vậy phương trình đường thẳng đi qua hai điểm cực trị của hàm số đã cho là: y=2x−m2+m.
 Phương Trình Đi Qua 2 Điểm Cực Trị
Phương Trình Đi Qua 2 Điểm Cực Trị Như vậy trên đây Hocvn đã hướng dẫn bạn Viết Phương Trình Đi Qua 2 Điểm Cực Trị Của Đồ Thị Hàm Số Bậc 3. Hi vọng bài viết hữu ích với bạn.

